Mean Median Mode and Range Practice to Review Chapter 14&15 Graph and Analyze Data
Finding the Hateful, Median, Mode and Range
The 3 distinct calculations associated with the Measure of Central Trend are the Mean, Median, and Way. Each measurement is an endeavor to capture the essence of how a typical entry or number in the data set may await similar. The idea is to compute a single value that tin represent the entire elements of the set.
In this lesson, I have prepared 8 (8) worked examples to illustrate how to perform the required computations.
Measures of Primal Tendency
Let's start go over the chief ideas of each mensurate of the central trend.
MEAN
Clarification:
"Average" value of the set of numbers
How to detect…
Add all numbers to go a total, then divide by the number of entries (number count of values you added).
Advantages:
- Takes into business relationship every number in the data set. That means all numbers are included in calculating the mean.
- Easy and quick way to correspond the unabridged data values by a single or unique number due to its straightforward method of calculation.
- Each ready has a unique hateful value.
Disadvantages:
Its value is easily affected past extreme values known as the outliers.
MEDIAN
Description:
Middle value of the set up of numbers
How to notice…
- Organize the numbers in increasing order, the median is the middle or centermost number.
- If at that place are ii middle numbers, add them and carve up by ii to get the median.
Advantages:
- Non afflicted by the outliers in the data set up. An outlier is a data point that is radically "distant" or "away" from common trends of values in a given set. It does not represent a typical number in the prepare.
- The concept of the median is intuitive thus can hands be explained as the center value.
- Each fix has a unique median value.
Disadvantages:
Its value is perceived as it is. Information technology cannot be utilized for further algebraic treatment.
MODE
Clarification:
Most common or frequent value or item of the gear up
How to observe…
Tally or count how many times a number appears in the list of information. The manner is the one that shows the about.
Advantages:
- Just similar the median, the mode is not affected by outliers.
- Useful to find the most "popular" or common item. This includes data sets that do not involve numbers.
Disadvantages:
If the set contains no repeating values, the mode is irrelevant. In contrast, if in that location are many values that have the aforementioned count, then mode can be meaningless.I did not include the range in the tabs to a higher place considering it is non really a measure out of cardinal tendency. However, the concept of range is usually discussed alongside with Mean, Median, and Mode. So, what is it and then?
RANGE
Range (in statistics) is the departure between the maximum and minimum value of the set up. What the range provides is a quick and rough estimate of the spread of data values within a set.
Consider the two scenarios below. Here we have 2 classes taking Algebra 1 and the ages of the students in each class.
- Algebra Form A
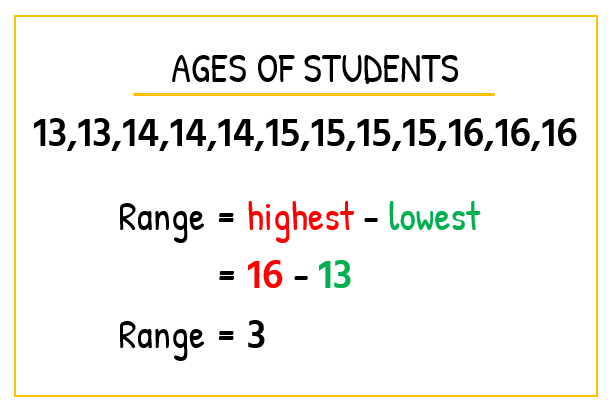
- Algebra Class B

Observations :
- Since the range of Form A is smaller than in Course B, can nosotros claim that the historic period distribution in Form A is more amassed (closely related) than in Grade B? In other words, are the ages listed in Class A more than uniform than in Class B?
Not so fast! This is, in fact, the biggest limitation of using the range to describe the spread of information within a set. The reason is that it can drastically be affected by outliers (values that are non typical every bit compared to the remainder of the elements in the fix).
- Notice that when nosotros condone the outliers in Class B (ages eleven and 18), the "new" range becomes…

…which is now equal to the range of Class A. So the "big have" from this case is to be very careful when interpreting the values of the range, particularly when comparison two sets.
Examples of How to Find the Mean, Median, Style, and Range
Instance 1: Observe the hateful, median, fashion and range for the following list of values
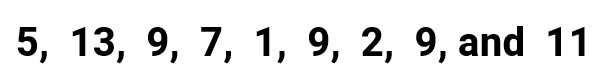
The mean is commonly known as the "average" which is calculated by getting the sum of all values in the list and and then divided by the number of entries. The symbol used to represent mean is \bar Ten, oftentimes read equally "x-bar".
- To discover the mean:

I rounded off the final answer to the nearest whole number because all the numbers in the ready are also whole numbers. To be more than specific, I rounded off the mean to the nearest "ones" place or digit.
Rounding off is an approximation so I use the wavy equal symbol \left( \approx \correct) to suggest that it is an guess and not an verbal answer. However, be proactive by request your teacher how many decimal places to round off your final reply.
- To notice the median:
I must organize the numbers from lowest to highest, and identify the "middle" value.
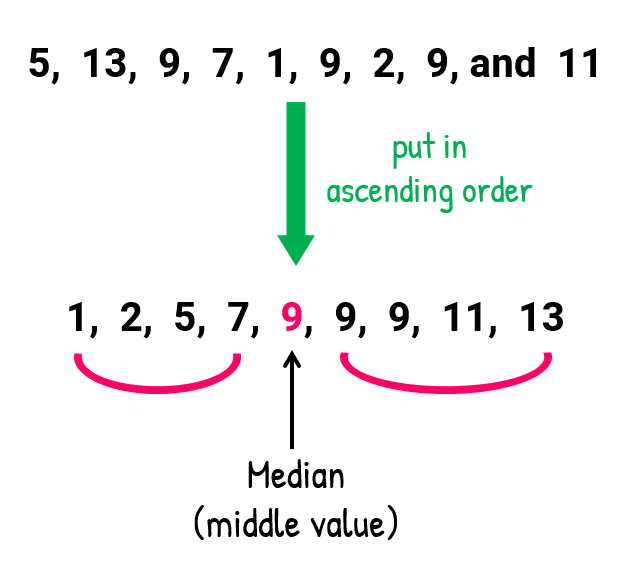
In addition, since the number count of entries is odd, information technology is guaranteed to have a middle value. A quick shortcut to decide which entry is the median is to add the number of entries (call it x) past 1 then divide past 2. Apply the output value hither to count from either the left or correct of the ordered list to pinpoint the exact location of the median.

From our previous trouble, the number of count of elements in the prepare is 10 = 9 and then we have
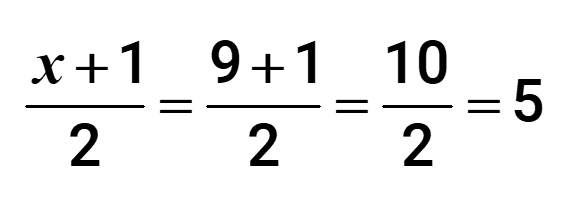
Therefore, the median is located by finding the vth entry when counted from either the left or right of the ordered listing.
- To find the mode:
The mode is the number in the list that appears the most, which in this case, the number 9. This number is repeated three times.
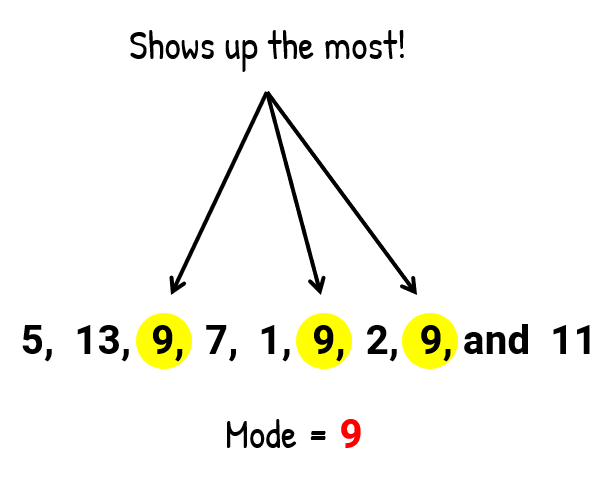
- To observe the range:
We don't need to organize the listing into numerical society to discover the lowest and highest values. You lot should be able to option those required ii values by quick inspection.
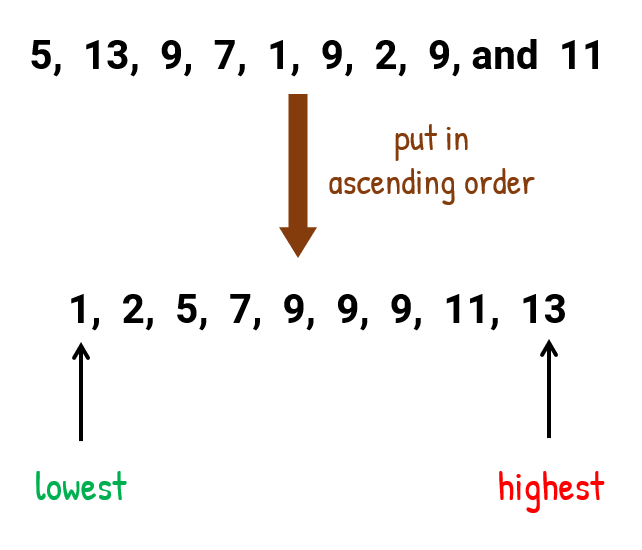
Since the range is the divergence between the highest and lowest value, thus, range = highest − lowest = 13 − one = 12.
Example two: Discover the hateful, median, manner and range for the following list of values
- To find the mean:
Another fashion to solve for the mean is to apply the formula
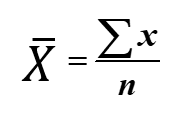
where the numerator is read equally "the summation of all ten values", and the denominator n is just the number count of values in a set up.
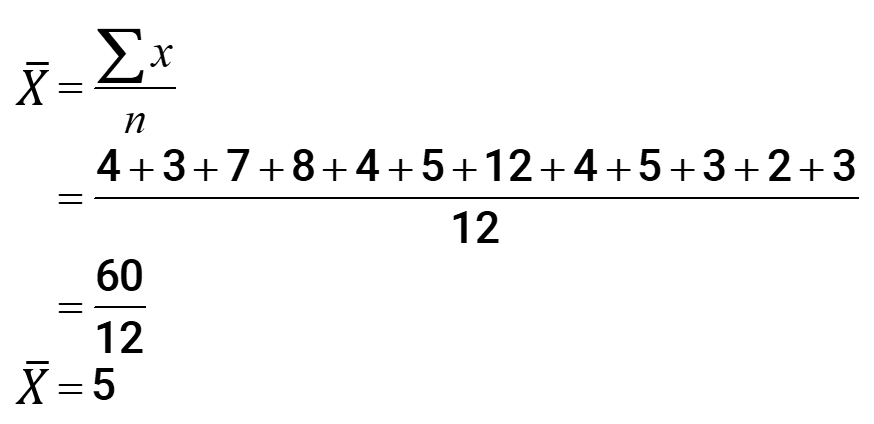
- To detect the median:
If we list the values in numerical guild, the median is establish at the "centermost" location. But here nosotros take no single value at the center of the list. To address this consequence, we are going to solve for the median past finding the average or mean of the two heart values.
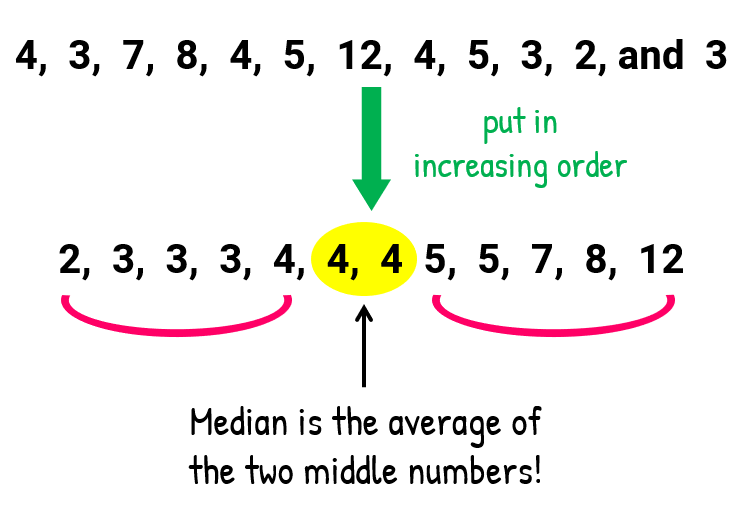
It just happens that the two center values are the aforementioned, therefore the average of two equal numbers will equal the same number.
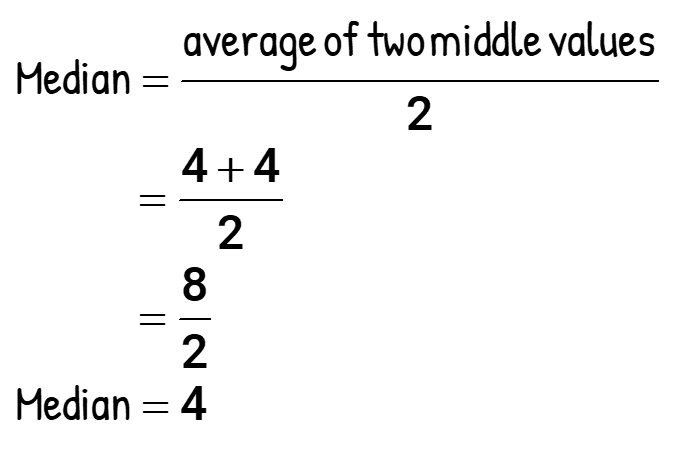
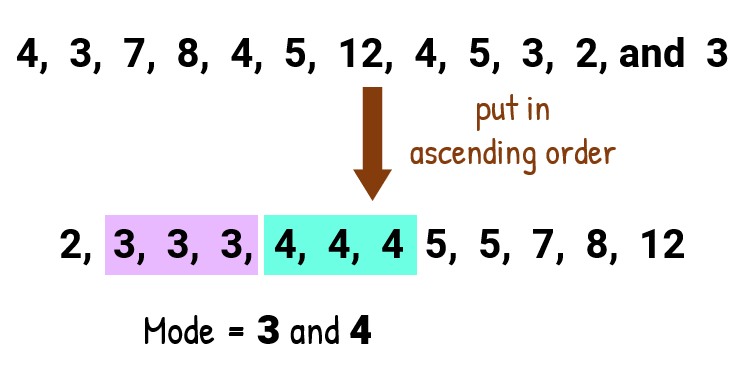
- To find the mode:
By quick inspection, we should observe that ii numbers (iii and 4) announced most frequently on the list. Tin we say that we have a tie because they both repeat iii times on the list? That precisely is the instance. Nosotros have a situation hither where two modes exist! Some textbook would call this set bimodal, that means having two modes.
- To discover the range:
Range is equal to maximum value minus minimum value which gives the states: 12 − ii = 10.
Example three: Find the mean, median, mode and range for the post-obit list of values
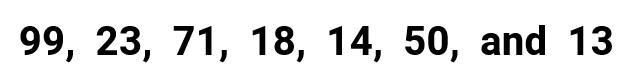
To determine the value of the mean, obtain the full of all the numbers and then divide past the number of numbers in the list. Since all given values are whole numbers, then information technology makes sense to have the final answer likewise expressed equally a whole. Therefore, I volition circular information technology off to the nearest ones' place.
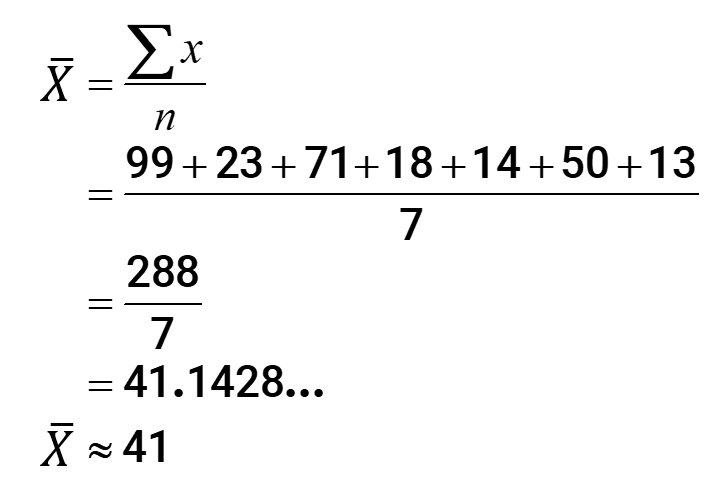
To solve for the median, let's arrange the list in increasing order and and then pick the center value. Patently, the median here equals 23.
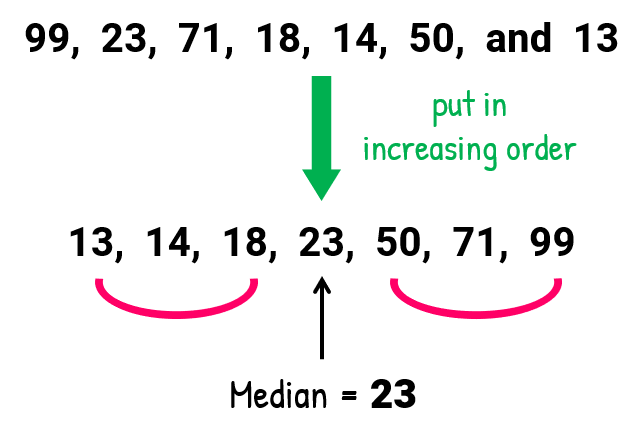
To solve for the mode, identify the almost "pop" value or entry in the list. Is there an element that appears more frequently in the listing?
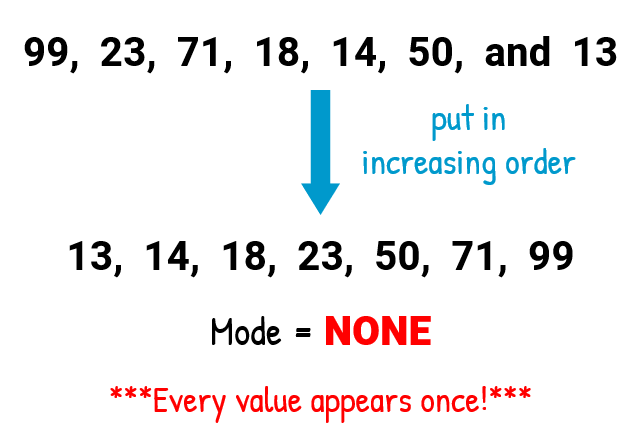
It is apparent that no value is repeated more often than the other. In fact, each unique number only shows upwardly one-fourth dimension. So, this set has no style.
The range is the easiest to find, Range = highest value minus everyman value. This gives us RANGE = 99 − 13 = 86.
Example 4: Notice the hateful, median, manner and range for the post-obit list of values
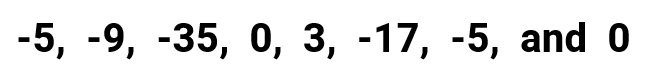
This is an interesting example because the elements in the ready now contain zeroes, a positive, and negative numbers. However, the methods that are used to solve for the mean, median, fashion and range practise non change.
- So for the m ean , I volition solve it equally usual past finding its "boilerplate". Since we are dealing with negative numbers, it is a good practise to place them inside the parenthesis to caution us to exist careful in combining them. Round off your answer to the nearest ones' place.
![average = [(-5)+(-9)+(-35)+0+3+(-17)+(-5)+0]/8 = -68/8 = -8.5](https://www.chilimath.com/wp-content/uploads/2019/06/mean-or-average-of-eight-negative-numbers.png)
- For the median , we need to be careful in rearranging the numbers in increasing guild because of the negative numbers. Remember that aught is e'er greater than whatever negative numbers. More then, to compare which of the 2 negative numbers is greater than the other, nosotros need to compare both using their accented values. The negative number with the smaller absolute value is the larger number!
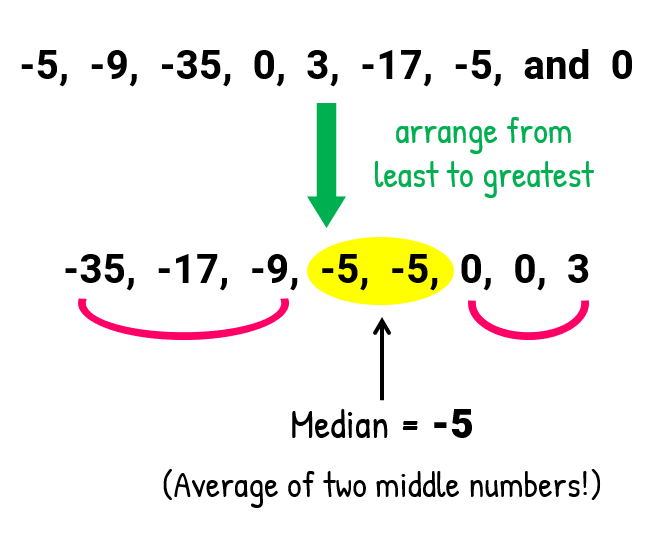
Information technology just happens that the 2 middle numbers are equal. Thus, their boilerplate will simply exist the number itself.
- For the way, find the elements of the set that appears more often. It looks like nosotros also take a tie! Both − five and 0 repeat itself twice. The modes
and then are − 5 and 0.
- The range is computed as follows:
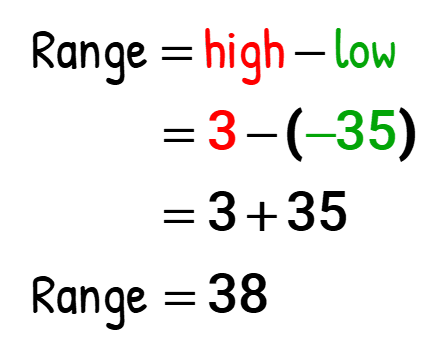
Retrieve that ii negative signs turn out to be positive. Make sure that you always remember this uncomplicated rule to prevent any unnecessary algebraic mistake.
Case 5: Discover the mean, median, mode and range for the post-obit listing of values
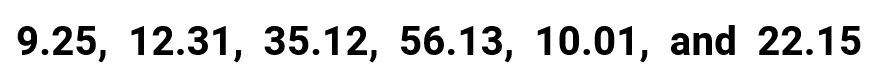
This example contains a set wherein all numbers have two decimal places. The dominion of thumb is to ensure that whatever results of our computations must likewise be rounded off to the same decimal places. Once more, information technology wouldn't hurt if yous ask an advice from your teacher how many decimals to round off every bit this role of the solution may exist open up to unlike interpretations.
- Finding the hateful:
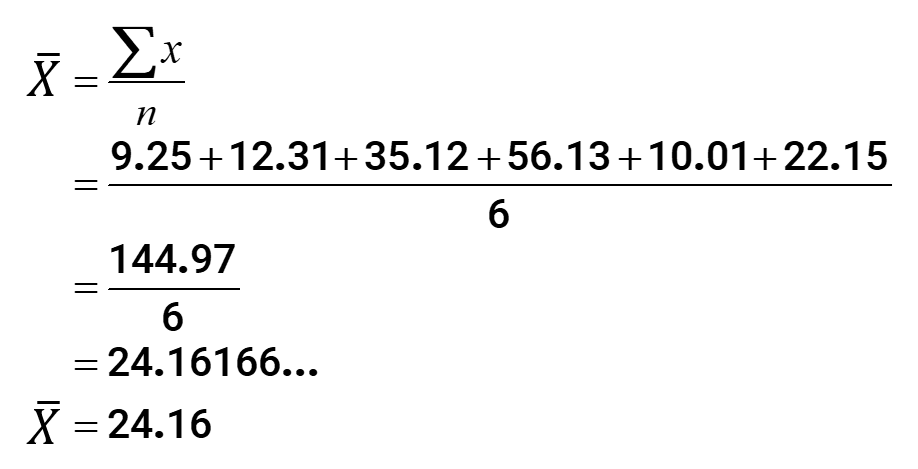
As you can see, I rounded off the last value of the mean to ii decimal places.
- Finding the median:
Adjust the numbers in increasing society – that is, from least to greatest. Past having an even number of entries in the set up suggests that we will have 2 middle numbers. This is always the case! You should anticipate getting the boilerplate of the two middle values to obtain the reply for the median.
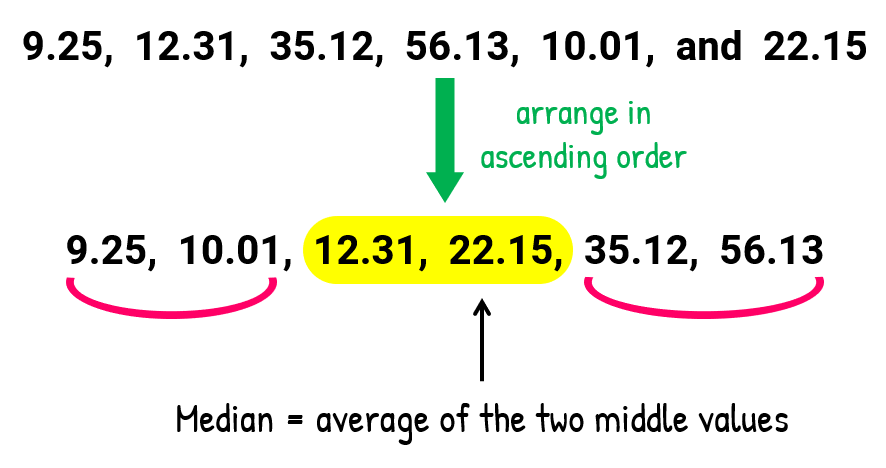
Here is the computation of the median…
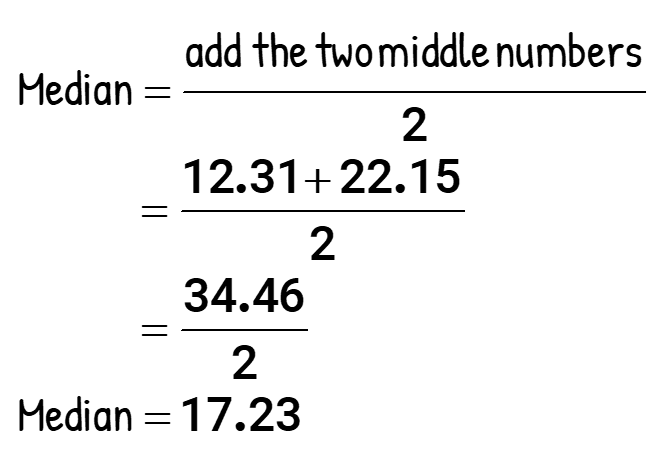
After dividing the sum of two heart numbers by 2 yields an answer with two decimal places. This is perfect! No need to practice some rounding off.
- Finding the mode:
Since each chemical element in the set appears just once (no repeating values), we say that this ready has no mode.
- Finding the range:
The highest value is 56.13, and while the lowest value is nine.25. The range is just the difference between them.
Range = 56.xiii − 9.25 = 46.88
Example 6: Notice the mean, median, manner and range for the following list of values
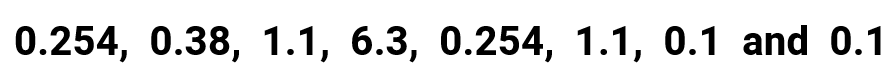
By quick inspection, the values in this prepare contain numbers that have different decimal places. Hopefully, y'all start by wondering how many decimal places should we round off the final answer. Again, this is open to interpretations. Therefore, I advise that you ask your teacher for further description.
NOTE: For this trouble though, I decided to round it off based on the number with the largest decimal places. I see that entry 0.254 contains iii digits later on the decimal point which is the biggest among others. And so accordingly, I will keep in mind to round off the final answer for the mean with iii digits after the decimal betoken.
- Determining the mean:
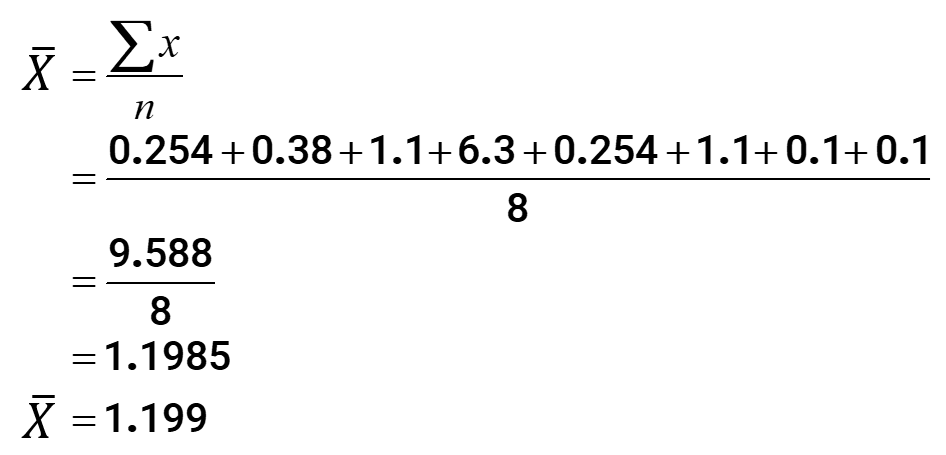
- Determining the median :
Similar to case five, this set has an even count of entries. Await to average the middle 2 values to solve for the median. Retrieve to round off your answer to the nearest three decimal places just like when we solved for the mean.
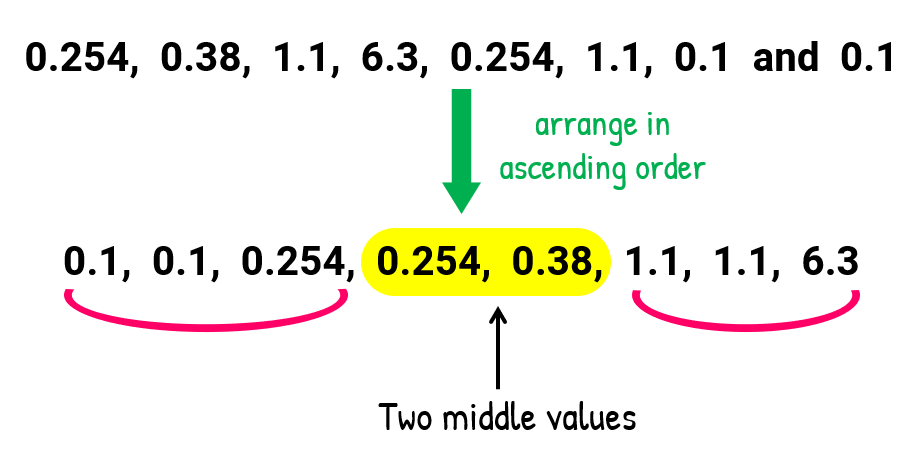
Here is the calculation for the median…

- Determining the mode:
Nosotros accept 3 modes (trimodal) in this set which are 0.one, 0.254 and 1.ane. They all repeat twice on the list!
- Determining the range:
The maximum value in the list is half dozen.3, and while the minimum value is 0.ane. Therefore the range is computed as follows…
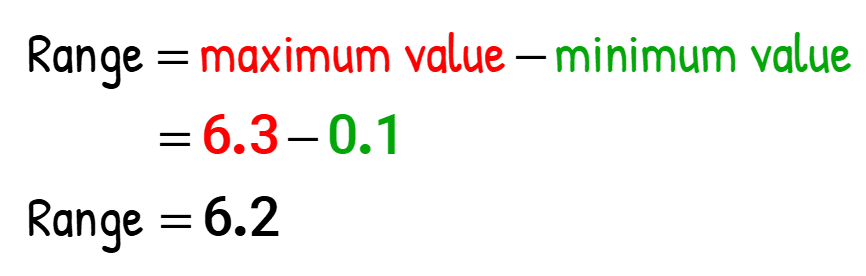
Case 7:Leroy wants to reach an overall grade of B in his quizzes. Currently, he has the following scores from his previous eleven quizzes: 75, 83, 96, 86, 69, 74, 83, 86, 90, 60 and lxxx. What should be his next score in guild to go a quiz average of eighty?
Let "x" exist the unknown exam score that Leroy needs to become. In guild to gear up the correct boilerplate, we need to make an adjustment on the number of entries being added: that is, from 11 to 12.
The working equation that can solve for the missing value of "x" is the following…
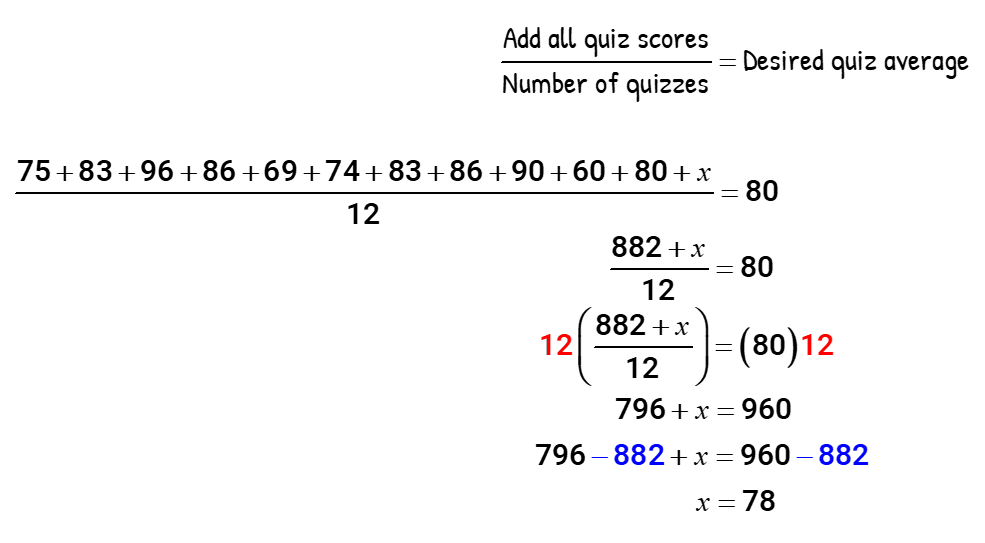
Leroy needs to score 78% on his side by side quiz in order to go a quiz average of fourscore%.
Example 8:Lisa is aware that she needs to accept five major exams in the semester. Unfortunately, due to medical reasons, she is only able to accept two exams with the scores of 85 and 89. To adapt her, the professor gives her a make-upward exam that would count as iii exam grades. What score does she need to get on this make-upwards exam to garner a ninety% average in all exams?
Solution:
Assign a variable to the unknown score. Let'southward call it "y". The total number of exams is 5 because of her existing 2 test scores which is added to the make-upwardly exam that is counted as 3. The desired equation to solve for the required score is…

Lisa needs to score 92% on this single exam that'south counted as three test grades to achieve an overall exam of 90%.
Practise with Worksheets
Source: https://www.chilimath.com/lessons/intermediate-algebra/mean-median-mode-and-range/
Enregistrer un commentaire for "Mean Median Mode and Range Practice to Review Chapter 14&15 Graph and Analyze Data"